
Using the staggered FDTD grid shown in the figure above, the electric field (blue grid points) are evaluated at integer spatial indices …, i – 1, i, i + 1, … and integer temporal indices …, n – 1, n, n + 1, … while the magnetic field (red grid points) are evaluated at half-integer spatial indices …, i – 1/2, i + 1/2, … and half-integer temporal indices …, n – 1/2, n + 1/2, … Therefore in the FDTD method, we discretize the equations using a staggered spatial and temporal grid as shown in the figure below, which allows us to numerically approximate the simultaneous solving of both coupled equations. This is obviously an impossible task when dealing with a numerical solution. Theoretically, the coupled equations must be solved simultaneously. Now that we know which equations to solve numerically, we need to discretize the pair of coupled electric field and magnetic fields.

In the first pair, we only have E z and B y:Īnd in the second pair we only have B z and E y:Īs both coupled pairs are essentially the same system when considering spatial and temporal symmetry, we only need to choose and implement one pair numerically in order to implement the 1D FDTD algorithm. These four equations can be rearranged as the following pair of coupled partial derivative equations. Once again for a 1 dimensional system, this reduces to the two equations: Where B k is the k th spatial component of the magnetic field. The third equation can be written out more clearly as: In order to implement the FDTD algorithm, we only need to use the third and fourth equations. Where Ḃ and Ė are the time derivatives of the magnetic field and electric field respectively.
Python fdtd how to#
In this post, we will explore how to implement the one dimensional electromagnetic FDTD algorithm in Python.Īs this post focuses on electromagnetism, we start from Maxwell’s equations in Gaussian units, and scale the units such that the value of the speed of light c = 1, and assume that no current J is present in the system: Such equations are impossible to solve analytically for complex systems such as random lasers or volcanic systems, and scientists have to make use of numerical methods to better understand how such systems behave under various conditions. The finite difference time domain (FDTD) algorithm is a numerical method used to solve partial differential equations which have both spatial and temporal derivatives such as Maxwell’s equations or seismic waves propagating through the earth. Please check here for the latest version of this post.
Python fdtd code#
Update: due to various difficulties encountered in writing Python code and mathematical equations in WordPress, I have decided to start migrating most of my content to Github. Running time:Problem dependent (a simulation with real valued electromagnetic field takes typically about 0.16 μs per Yee cell per time-step.)References:SWIG.
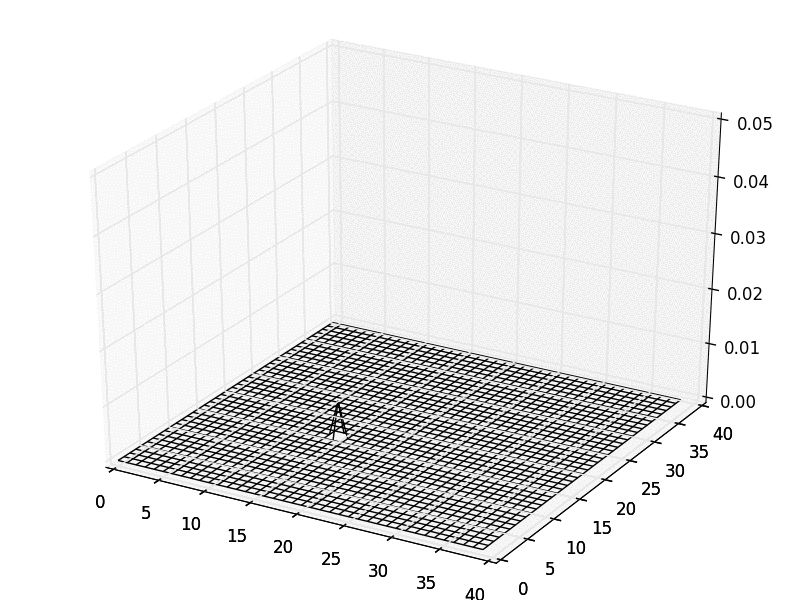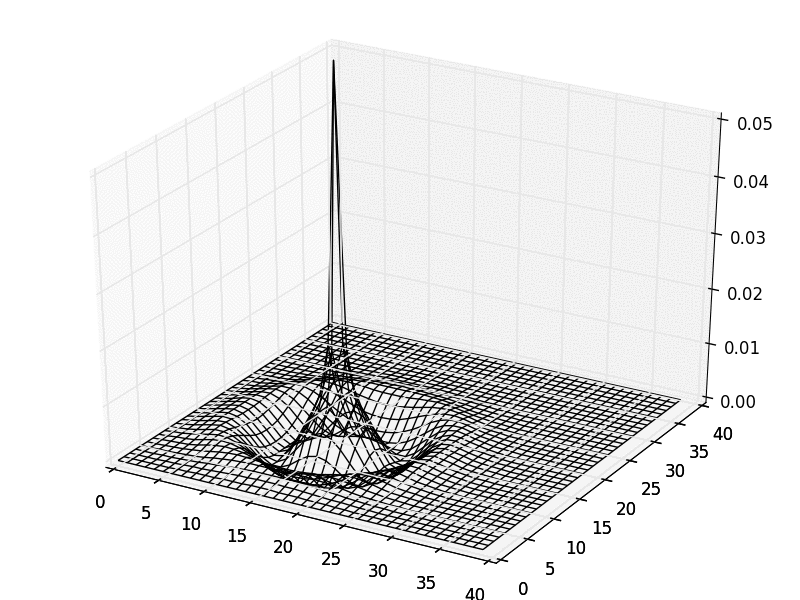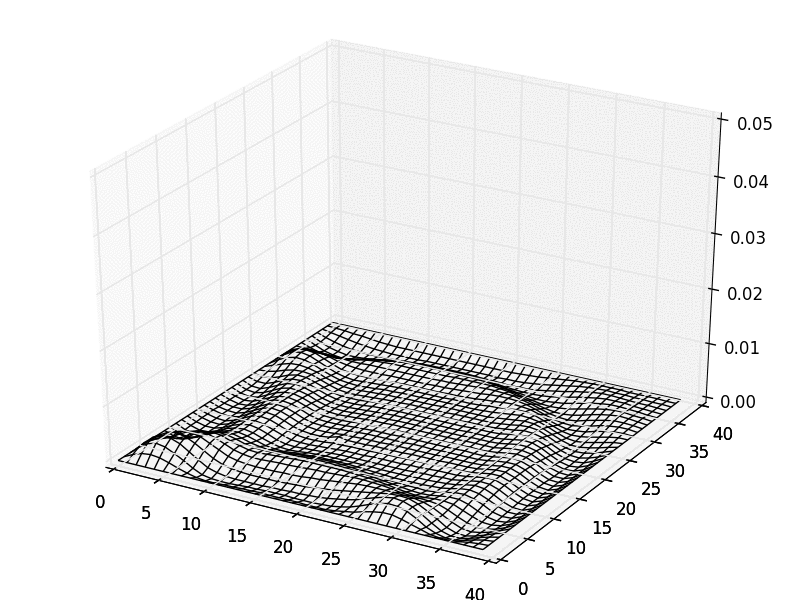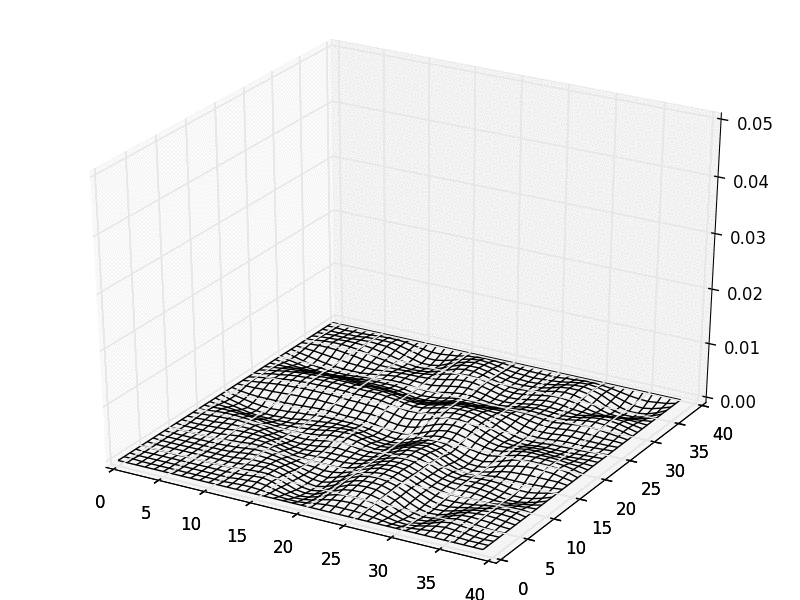
The most recent version can be downloaded at the GMES project homepage. Parallelized with MPI directives (optional).RAM: Problem dependent (a simulation with real valued electromagnetic field uses roughly 0.18 KB per Yee cell.)Classification: 10.External routines: SWIG, Cython, NumPy, SciPy, matplotlib, MPI for Python Nature of problem: Classical electrodynamicsSolution method:Finite-difference time-domain (FDTD) methodAdditional comments:This article describes version 0.9.5. of bytes in distributed program, including test data, etc.: 89878Distribution format: tar.gzProgramming language: C++, Python.Computer: Any computer with a Unix-like system with a C++ compiler, and a Python interpreter developed on 2.53 GHz Intel Core TM i3.Operating system: Any Unix-like system developed under Ubuntu 12.04 LTS 64 bit.Has the code been vectorized or parallelized?: Yes. of lines in distributed program, including test data, etc.: 17700No.
Python fdtd license#
IrelandLicensing provisions: GNU General Public License v3.0No. The key design features, along with the supported material types, excitation sources, boundary conditions and parallel calculations employed in GMES are also described in detail.Program title: GMESCatalog identifier: AEOK_v1_0Program summary URL: obtainable from: CPC Program Library, Queen’s University, Belfast, N. The users can easily add various material types, sources, and boundary conditions into their code using the Python programming language. This piecewise updating scheme ensures that GMES can adopt OOP without losing its simple structure and time-stepping speed. The design of GMES follows the object-oriented programming (OOP) approach and adopts a unique design strategy where the voxels in the computational domain are grouped and then updated according to its material type.

Python fdtd free#
This paper describes GMES, a free Python package for solving Maxwell’s equations using the finite-difference time-domain (FDTD) method.


 0 kommentar(er)
0 kommentar(er)
